One of the best laws for analyzing a circuit is Kirchhoff’s law. There are two different Kirchhoff’s laws:
- Kirchhoff’s current law
- Kirchhoff’s voltage law
The basic foundation for Kirchhoff’s current law was formed from the works of Georg Ohm’s who states Ohm’s laws while the foundation for Kirchhoff’s voltage law was formed from the works of Gustav Robert Kirchhoff himself.
The article explains what is Kirchhoff’s law, what are the types, advantages and limitations of Kirchhoff’s law and its applications.
What is Kirchhoff’s law?
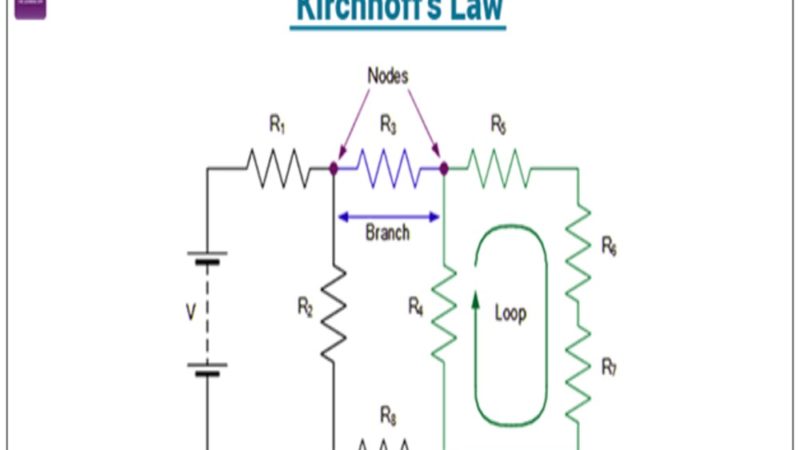
There are two equations that are addressed in the laws of Kirchhoff’s and they are conservation of energy and conservation of charge, with respect to electrical circuits. These two equations are important when it comes to complex circuits such as bridge networks or T networks. These networks are used for calculating either the voltage or current. Using only Ohm’s law won’t help much.
Introduction to Kirchhoff’s laws of current and voltage
The main law can be divided into first and second laws. That is:
- Kirchhoff’s Current Law (KCL) or Kirchhoff’s first law
- Kirchhoff’s Voltage Law (KVL) or Kirchhoff’s second law
Kirchhoff’s first law
According to Kirchhoff’s first law, also known as Kirchhoff’s current law, the total current or charge entering the junction is equal to the current or charge that is leaving from the junction. It is also stated as the sum of all the currents entering an electric network is equal to zero.
When the current or charge flows towards the network, it is considered to be positive and when the current or charge flows outside the network, it is considered to be negative. Therefore, the mathematical way of expressing the statement is as follows:
Iin + Iout = 0
Kirchhoff’s second law
According to Kirchhoff’s second law, also known as Kirchhoff’s voltage law, in any closed electrical circuit, the sum of emf values is equal to the sum of potential drops in the circuit.
The other way of stating the second law is the voltage around the loop is equal to the sum of all the voltage drops within the loop, which is equal to zero.
Consider an electric loop with A, B, C and D as the four nodes with an R resistor. Then, according to Kirchhoff’s second law, the mathematical expression for the electric loop is given as:
VAB + VBC + VCD + VDA = 0
Advantages and limitations of Kirchhoff’s law
Advantages:
- With the help of this law, determining the unknown current and voltage becomes simple and easy.
- The analysis of complicated electric loops becomes doable.
Limitation:
- The only limitation of Kirchhoff’s law is that before calculation of unknow value of current and voltage, it is assumed that there is no fluctuation in the magnetic field of the electric loop.
Interested to learn more about other laws of Physics such as Bragg’s law, Newton’s laws of motion, etc, stay tuned with BYJU’S or do visit our YouTube channel for more interesting videos.